2020-05-03
Path finding using a navmesh
This post covers generating smooth path from a two-dimensional navmesh in Javascript.
Part of series about 2D navigation meshes:
Setup
We’re starting from a navmesh generated in the previous post. Also on the map are marked our path’s starting and goal positions.
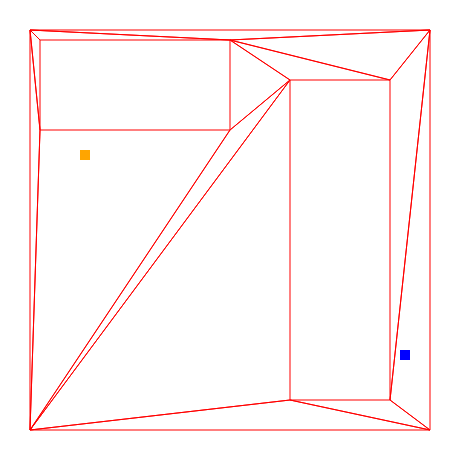
Our goal is to find the smoothest path to travel from the orange dot to the blue one.
Edgefinding
We’re dealing with a set of triangles, so the first step of path finding can be summed up as finding the triangles to traverse. The “triangle-path-finding” consists of these steps:
- Find the triangle containing the start point and the triangle containing the end point
- Build a graph with individual triangles as nodes and triangles sharing sides as edges
- Use a standard path finding algorithm, such as Dijkstra’s, to find the sequence of triangles to traverse from the start point’s triangle to the end point’s triangle
- Since an edge in the graph represents a navmesh triangle’s edge, we can compose a path of navmesh edges from a sequence of graph edges
Step 1: find the triangles that contain start point and end point
function findTriangleContaining(
indices: number[],
vertices: number[],
point: Point
) {
let i = 0;
for (const triangle of triangles(indices, vertices)) {
if (triangleContainsPoint(triangle, point)) {
return i;
}
i++;
}
}
const startTriangle = findTriangleContaining(
indices,
mapVerts,
startPos
);
const endTriangle = findTriangleContaining(
indices,
mapVerts,
endPos
);
Step 2: graph building
The core of turning our navmesh into a graph is finding neighbours for each navmesh triangle. Since our triangulation method provided us with a list of indices, finding neighbours is as easy as finding the other triangles that share at least two vertices with the current triangle.
type Node = { id: number; neighbours: Node[] };
const graph: Node[] = [];
const tIndices = [...triangleIndices(indices)];
// First step: add all triangles
for (let i = 0; i < tIndices.length; ++i) {
graph.push({ id: i, neighbours: [] });
}
// Second step: find neighbours
for (const [triangle, indices0] of tIndices.entries()) {
const neighbours = [...tIndices.entries()]
.filter(([nTriangle, indices1]) => {
return (
nTriangle !== triangle &&
doTrianglesShareEdge(indices0, indices1)
);
})
.map(([nTriangle]) => graph[nTriangle]);
graph[triangle].neighbours = neighbours;
}
We can test it out by drawing the neighbours for both the start and the end point’s triangles.

const startAndEndNeighbourIndices = [
...graph[startTriangle].neighbours,
...graph[endTriangle].neighbours,
].flatMap(({ id }) => {
return [
indices[id * 3 + 0],
indices[id * 3 + 1],
indices[id * 3 + 2],
];
});
drawTriangles(startAndEndNeighbourIndices, mapVerts);
Step 3: finding the path of edges
Only thing that remains is finding the path. For sake of simplicity we’ll just use a package for A-star. If you’re interested in learning more about path finding in-depth, Amit’s A* Pages is an excellent resource.
function triangleMidPoint(triangleIndex) {
const tIndices = [
indices[triangleIndex * 3 + 0],
indices[triangleIndex * 3 + 1],
indices[triangleIndex * 3 + 2],
];
const x =
tIndices.reduce(
(prev, cur) => prev + mapVerts[cur * 2 + 0],
0
) / 3;
const y =
tIndices.reduce(
(prev, cur) => prev + mapVerts[cur * 2 + 1],
0
) / 3;
return [x, y];
}
const { path } = astar({
start: startTriangle,
isEnd: (n) => n === endTriangle,
neighbor: (n) => graph[n].neighbours.map((n) => n.id),
distance: (a, b) => {
const [ax, ay] = triangleMidPoint(graph[a].id);
const [bx, by] = triangleMidPoint(graph[b].id);
const [dx, dy] = [ax - bx, ay - by];
return Math.sqrt(dx * dx + dy * dy);
},
heuristic: (n) => {
// Euclidean distance
const [nx, ny] = triangleMidPoint(graph[n].id);
const dx = nx - endPos[0];
const dy = ny - endPos[1];
return Math.sqrt(dx * dx + dy * dy);
},
});
The end result we get is the triangles forming the shortest path from the start to the end triangle, here highlighted in green.
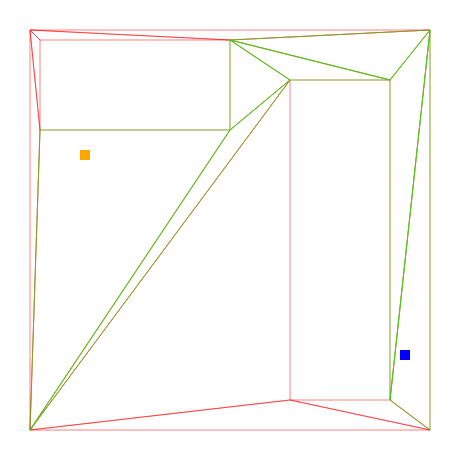
We’re already getting somewhere, but our “path” is still too coarse. Rather than knowing the triangles we need to walk through, we should find the triangle edges we should pass through. We already almost have this information stored in our path array; we just need to map a pair of triangles [fromTriangle, toTriangle] into the edge in between.
function* pathToEdges(path, graph) {
for (let i = 1; i < path.length; ++i) {
const fromTriangle = graph[path[i - 1]].id;
const toTriangle = graph[path[i]].id;
const tri0 = [
indices[fromTriangle * 3 + 0],
indices[fromTriangle * 3 + 1],
indices[fromTriangle * 3 + 2],
];
const tri1 = [
indices[toTriangle * 3 + 0],
indices[toTriangle * 3 + 1],
indices[toTriangle * 3 + 2],
];
// Find vertices in both triangles. MUST have length of 2
const sharedVertices = tri0.filter((i) =>
tri1.includes(i)
);
const vert0 = [
mapVerts[sharedVertices[0] * 2 + 0],
mapVerts[sharedVertices[0] * 2 + 1],
];
const vert1 = [
mapVerts[sharedVertices[1] * 2 + 0],
mapVerts[sharedVertices[1] * 2 + 1],
];
yield [vert0, vert1];
}
}
const pathVertices = [...pathToEdges(path, graph)];

Edges into path
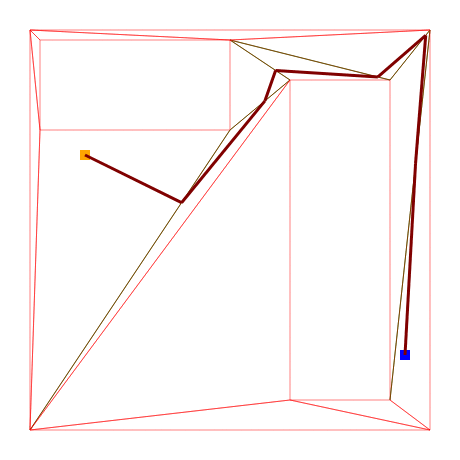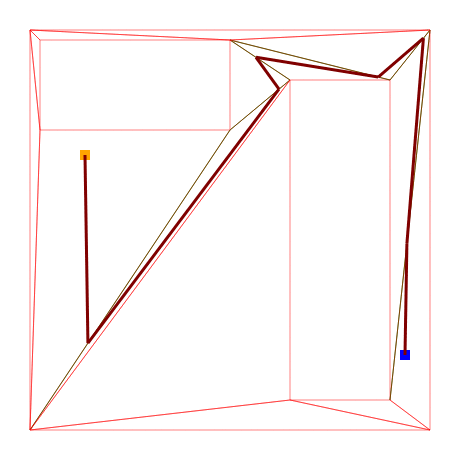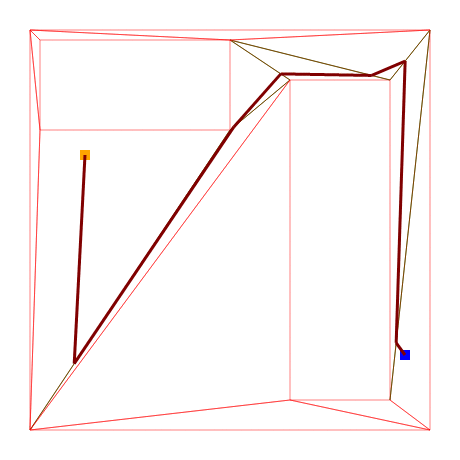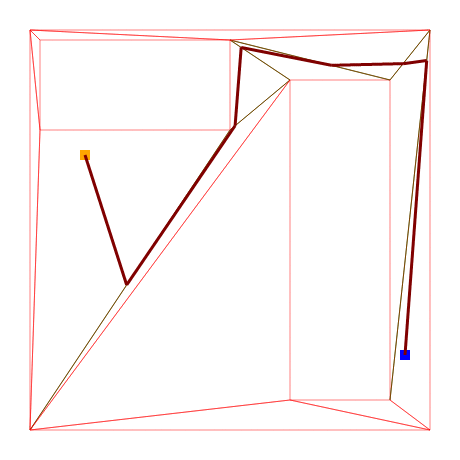
We know the edges, but we want a path. Let’s start experimenting with a simple idea. Now we know what edges the actor will have to pass through to traverse our chosen path, so what if we just link the middlepoints of each edge together?

The path does not look clean or fast, but importantly it is still a correct path. We just found our first walkable path!
This also leads us to another realization: since we chose to use triangles for our polygon tessellation and triangles are by definition convex, we can freely move our path nodes to any part of their respective edge while still having a valid path.
Let’s use this to our advantage with some heuristical shifting around.
Path optimization
Let’s simplify the problem:
We have an array W, containing weights for each edge. Weight here essentially means how far is the vertex from the first vertex of the edge. (TODO add a demonstrative GIF)
We have a function length(W), which gives us the length of the whole path for given weights.
Our goal is to find the W for which the return value of length(W) is the lowest, or in mathy terms argmin length(W).
Our options are
- Brute force
- Gradient descent
Path optimization option a) brute force
This is the “screw math, CPU power is cheap” option. We’ll brute force 1000 random weights and choose the one giving us the shortest path.
let [shortestWeights, shortestDist] = [null, Infinity];
for (let i = 0;i < 1000; ++i) {
const weights = pathVertices.map(() => Math.random());
const length = lengthWithWeights(pathVertices, weights);
if (length < shortestDist) {
[shortestWeights, shortestDist] = [weights, length];
}
}
const pathPoints = pathWithWeights(
pathVertices,
shortestWeights
);
This is a reasonable option for many cases since it’s quite obvious what’s happening and relatively inexpensive operation. For more complex path finding cases, more thought might be applicable.
The results can be reasonably good as well:

Path optimization option b) gradient descent
This is where things get slightly more mathy. Let’s consider our situation: Some of you probably had a lightbulb appear: this is a good candidate for gradient descent.
As per wikipedia, gradient descent is an optimization method for finding the local minimum for a differentiable function. In other words, by calculating the derivative of our length(W) function and using gradient descent to find the values of W for which length(W) returns the minimum value, we’re able to find the edge weights for which we get the shortest path.
The first step is calculating the derivative for our length function. The mathematical definition of it would be something like length(W) = ΣS + (E - S)*w.
TODO
Appendix: utility functions used
Functions here have TypeScript types for understandability.
type Point = [number, number];
type Triangle = [Point, Point, Point];
function* triangleIndices(indices: number[]) {
for (let i = 0; i < indices.length; i += 3) {
yield [indices[i], indices[i + 1], indices[i + 2]] as [
number,
number,
number
];
}
}
function doTrianglesShareEdge(
indices0: [number, number, number],
indices1: [number, number, number]
) {
// If triangles A and B share two indices, they share an edge
let shared = 0;
for (const i of indices0) {
if (indices1.includes(i) && ++shared === 2) {
return true;
}
}
return false;
}
function* triangles(indices: number[], vertices: number[]) {
for (const [i0, i1, i2] of triangleIndices(indices)) {
const p0: Point = [
vertices[i0 * 2],
vertices[i0 * 2 + 1],
];
const p1: Point = [
vertices[i1 * 2],
vertices[i1 * 2 + 1],
];
const p2: Point = [
vertices[i2 * 2],
vertices[i2 * 2 + 1],
];
yield [p0, p1, p2] as Triangle;
}
}
// https://blackpawn.com/texts/pointinpoly/default.html
// https://github.com/mattdesl/point-in-triangle
function triangleContainsPoint(
triangle: Triangle,
testing: Point
) {
//compute vectors & dot products
const cx = testing[0],
cy = testing[1],
t0 = triangle[0],
t1 = triangle[1],
t2 = triangle[2],
v0x = t2[0] - t0[0],
v0y = t2[1] - t0[1],
v1x = t1[0] - t0[0],
v1y = t1[1] - t0[1],
v2x = cx - t0[0],
v2y = cy - t0[1],
dot00 = v0x * v0x + v0y * v0y,
dot01 = v0x * v1x + v0y * v1y,
dot02 = v0x * v2x + v0y * v2y,
dot11 = v1x * v1x + v1y * v1y,
dot12 = v1x * v2x + v1y * v2y;
// Compute barycentric coordinates
const b = dot00 * dot11 - dot01 * dot01,
inv = b === 0 ? 0 : 1 / b,
u = (dot11 * dot02 - dot01 * dot12) * inv,
v = (dot00 * dot12 - dot01 * dot02) * inv;
return u >= 0 && v >= 0 && u + v < 1;
}
function pathWithWeights(pathVertices, weights) {
return pathVertices.map(([v0, v1], i) => {
const w = weights[i];
return [v0[0] + (v1[0] - v0[0]) * w, v0[1] + (v1[1] - v0[1]) * w];
});
}
function dist(a, b) {
const [dx, dy] = [a[0] - b[0], a[1] - b[1]];
return Math.sqrt(dx * dx + dy * dy);
}
function lengthWithWeights(pathVertices, weights) {
const withWeights = pathWithWeights(pathVertices, weights);
const startToFirstDistance = dist(startPos, withWeights[0]);
const lastToEndDistance = dist(withWeights[withWeights.length - 1], endPos);
return withWeights.reduce(
([prev, pathDist], cur) => {
if (prev) {
pathDist += dist(cur, prev);
}
return [cur, pathDist];
},
[null, startToFirstDistance + lastToEndDistance]
)[1];
}